Tensão Induzida em Máquinas CA: Fundamentos Básicos
9/3/20252 min read
Continuação: Força Magnetomotriz e Distribuição de Fluxo - Parte II
Na primeira parte, exploramos a distribuição de fluxo e força magnetomotriz em máquinas CA reais. Agora vamos focar no cálculo da tensão induzida, começando pelos fundamentos mais simples.
A Equação Fundamental da Tensão Induzida
A tensão induzida em uma máquina CA pode ser expressa pela equação básica:
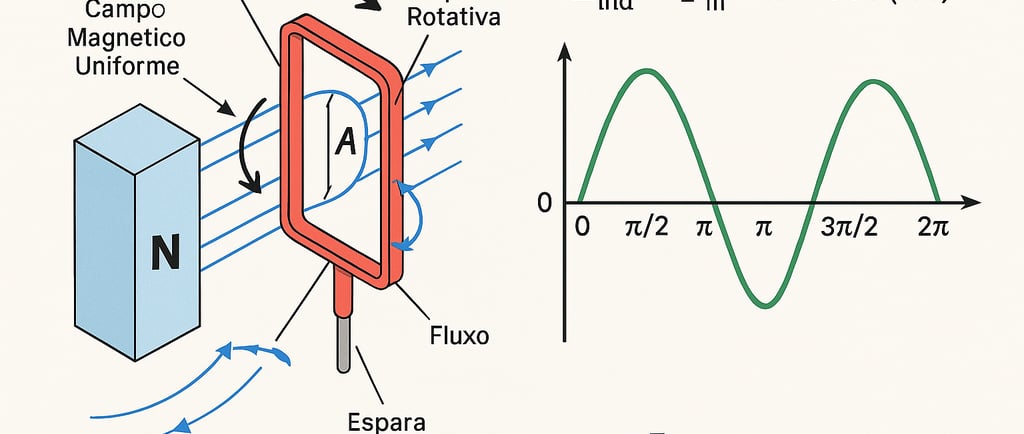
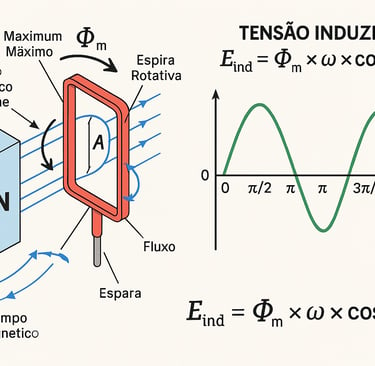
E_ind = Φ_m × ω × cos(ωt)
Onde:
E_ind = tensão induzida instantânea [V]
Φ_m = fluxo magnético máximo [Wb]
ω = velocidade angular [rad/s]
t = tempo [s]
Interpretação Física da Equação
1. Fluxo Máximo (Φ_m)
O fluxo magnético máximo representa a quantidade máxima de linhas de campo magnético que atravessam a área da espira quando ela está posicionada perpendicularmente ao campo.
2. Velocidade Angular (ω)
A velocidade angular determina a rapidez com que o fluxo varia no tempo. Quanto maior a velocidade, maior será a taxa de variação e, consequentemente, maior a tensão induzida.
3. Função Cosseno
A função cos(ωt) representa a variação senoidal do fluxo magnético concatenado conforme a espira (ou rotor) gira no campo magnético.
Dedução Simples da Equação
Partindo da Lei de Faraday:
E_ind = -dΦ/dt
Se o fluxo varia senoidalmente:
Φ(t) = Φ_m × sen(ωt)
Aplicando a derivada:
E_ind = -d/dt[Φ_m × sen(ωt)] E_ind = -Φ_m × ω × cos(ωt)
Por convenção de sinais (considerando o sentido de referência):
E_ind = Φ_m × ω × cos(ωt)
Parâmetros Práticos
Frequência e Velocidade Angular
ω = 2πf
Onde f é a frequência em Hz.
Valor Eficaz (RMS)
E_rms = Φ_m × ω / √2
Para 60 Hz (sistema brasileiro):
ω = 2π × 60 = 377 rad/s
Exemplo Prático Simples
Dados:
Fluxo máximo: Φ_m = 10 mWb = 0,01 Wb
Frequência: f = 60 Hz
ω = 377 rad/s
Cálculos:
Tensão instantânea:
E_ind(t) = 0,01 × 377 × cos(377t) = 3,77 × cos(377t) V
Valor eficaz:
E_rms = 3,77 / √2 = 2,67 V
Valor de pico:
E_pico = 3,77 V
Fatores que Influenciam a Tensão
1. Aumento do Fluxo Magnético
Material ferromagnético melhor
Campo magnético mais intenso
Área maior da espira
2. Aumento da Velocidade
Rotação mais rápida
Maior frequência de operação
3. Configuração Geométrica
Número de espiras
Área efetiva da bobina
Posicionamento relativo
Limitações da Equação Básica
Esta equação fundamental E_ind = Φ_m × ω × cos(ωt) é válida para:
Uma única espira em campo uniforme
Rotação constante
Campo magnético senoidal
Sem considerar perdas ou dispersões
Para Máquinas Reais:
Precisamos incluir fatores de correção como:
Fator de distribuição (k_d)
Fator de passo (k_p)
Número de espiras (N)
Efeitos de saturação
Próximos Passos
Esta equação básica E_ind = Φ_m × ω × cos(ωt) é o ponto de partida para:
Múltiplas espiras: multiplicar por N
Enrolamentos distribuídos: aplicar fatores k_d e k_p
Sistemas trifásicos: considerar defasagens de 120°
Máquinas reais: incluir correções práticas
Na próxima parte, expandiremos esta base para enrolamentos complexos e aplicações práticas em motores e geradores.
Artigo técnico do Blog Do Zero Ao Ohm - Fundamentos da Tensão Induzida em Máquinas CA
Equação Principal:
E_ind = Φ_m × ω × cos(ωt)
