Teorema de Norton: Simplificando Circuitos com Elegância
Quando nos deparamos com circuitos elétricos complexos, uma das ferramentas mais poderosas que temos à nossa disposição é o Teorema de Norton. Assim como seu "primo" Teorema de Thévenin, Norton nos oferece uma forma elegante de simplificar circuitos intrincados em equivalentes muito mais simples de analisar.
9/21/20252 min read
O que é o Teorema de Norton?
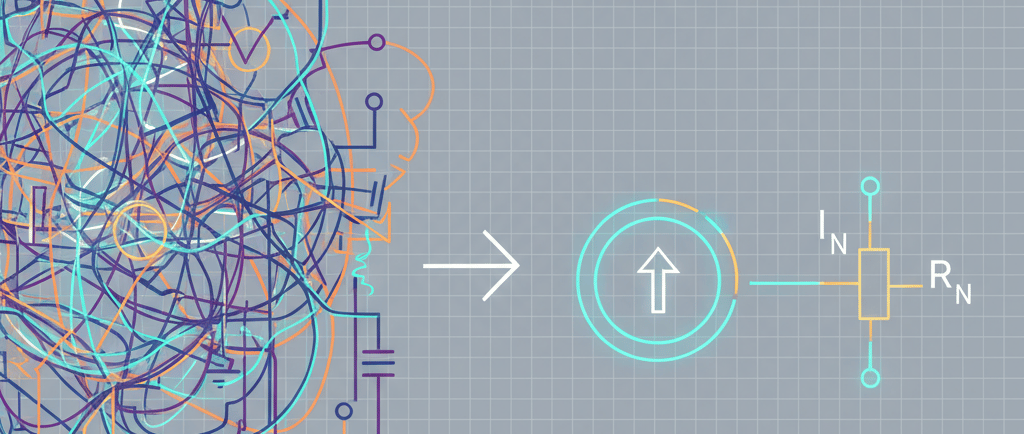
O Teorema de Norton estabelece que qualquer circuito linear com duas ou mais fontes pode ser substituído por um circuito equivalente contendo apenas:
Uma fonte de corrente (IN - corrente de Norton)
Uma resistência em paralelo (RN - resistência de Norton)
Esta simplificação mantém as mesmas características elétricas nos terminais externos, permitindo análises muito mais diretas.
Os Componentes do Circuito Equivalente Norton
1. Corrente de Norton (IN)
Um ponto fundamental do Teorema de Norton é que a corrente de Norton é definida quando os terminais de saída estão em curto-circuito. Assim, temos:
IN = ISC (corrente de curto-circuito)
Para encontrar a corrente de Norton:
Remova a carga dos terminais
Coloque um curto-circuito entre os terminais
Calcule a corrente que flui através deste curto
2. Resistência de Norton (RN)
A resistência de Norton é a resistência equivalente vista pelos terminais quando todas as fontes independentes são "desativadas":
Fontes de tensão → curto-circuito
Fontes de corrente → circuito aberto
RN = ROC = RTH
Onde:
ROC = resistência de circuito aberto
RTH = resistência de Thévenin
A Conexão entre Norton e Thévenin
Aqui está uma das belezas da teoria de circuitos: os teoremas de Norton e Thévenin se complementam perfeitamente!
Para encontrar os parâmetros de Norton, frequentemente utilizamos primeiro o método de Thévenin, pois:
Transformação Thévenin ↔ Norton
Se você conhece os parâmetros de Thévenin:
IN = VTH / RTH
RN = RTH
E vice-versa, se conhece Norton:
VTH = IN × RN
RTH = RN
Esta transformação de fonte é conhecida como transformação Thévenin-Norton e é extremamente útil na prática.
Quando Usar o Teorema de Norton?
O Teorema de Norton é particularmente útil quando:
✅ Você precisa analisar diferentes cargas conectadas aos mesmos terminais ✅ O circuito original tem muitas fontes de corrente ✅ Você quer uma perspectiva diferente do Thévenin para validar resultados ✅ Está projetando circuitos que serão conectados a cargas variáveis
Exemplo Prático
Imagine um circuito com múltiplas fontes alimentando uma carga resistiva. Em vez de recalcular correntes e tensões toda vez que a carga muda, você pode:
Determinar IN: calcular a corrente de curto-circuito
Encontrar RN: calcular a resistência equivalente
Aplicar o modelo: usar o circuito Norton equivalente para qualquer análise futura
A Importância na Análise de Circuitos
Os teoremas de Norton e Thévenin são fundamentais na análise de circuitos elétricos porque:
Simplificam problemas complexos
Aceleram os cálculos
Facilitam o entendimento do comportamento do circuito
Permitem análises rápidas com diferentes cargas
Conclusão
O Teorema de Norton não é apenas uma ferramenta matemática abstrata – é uma ferramenta prática que todo engenheiro e técnico em eletrônica deve dominar. Sua relação íntima com o Teorema de Thévenin cria um conjunto poderoso de técnicas que transformam análises complexas em cálculos diretos.
Lembre-se: um teorema complementa o outro. Dominar ambos é ter o controle completo sobre a análise de circuitos lineares!
No próximo post, veremos exemplos práticos de aplicação do Teorema de Norton em circuitos reais. Continue acompanhando o blog Do Zero ao Ohm!
Tags: #TeoremaDeNorton #AnaliseDeCircuitos #EletronicaBasica #Thevenin #TransformacaoDeFonte
